Our research focuses on understanding the fundamental mechanisms of failure in materials, encompassing brittle, quasi-brittle, and ductile solids. We aim to develop mechanistic models grounded in first-principle calculations, utilising a minimal set of parameters that can be directly measured experimentally. These models are designed to capture the complexities of material behaviour, particularly under conditions leading to fracture and failure.

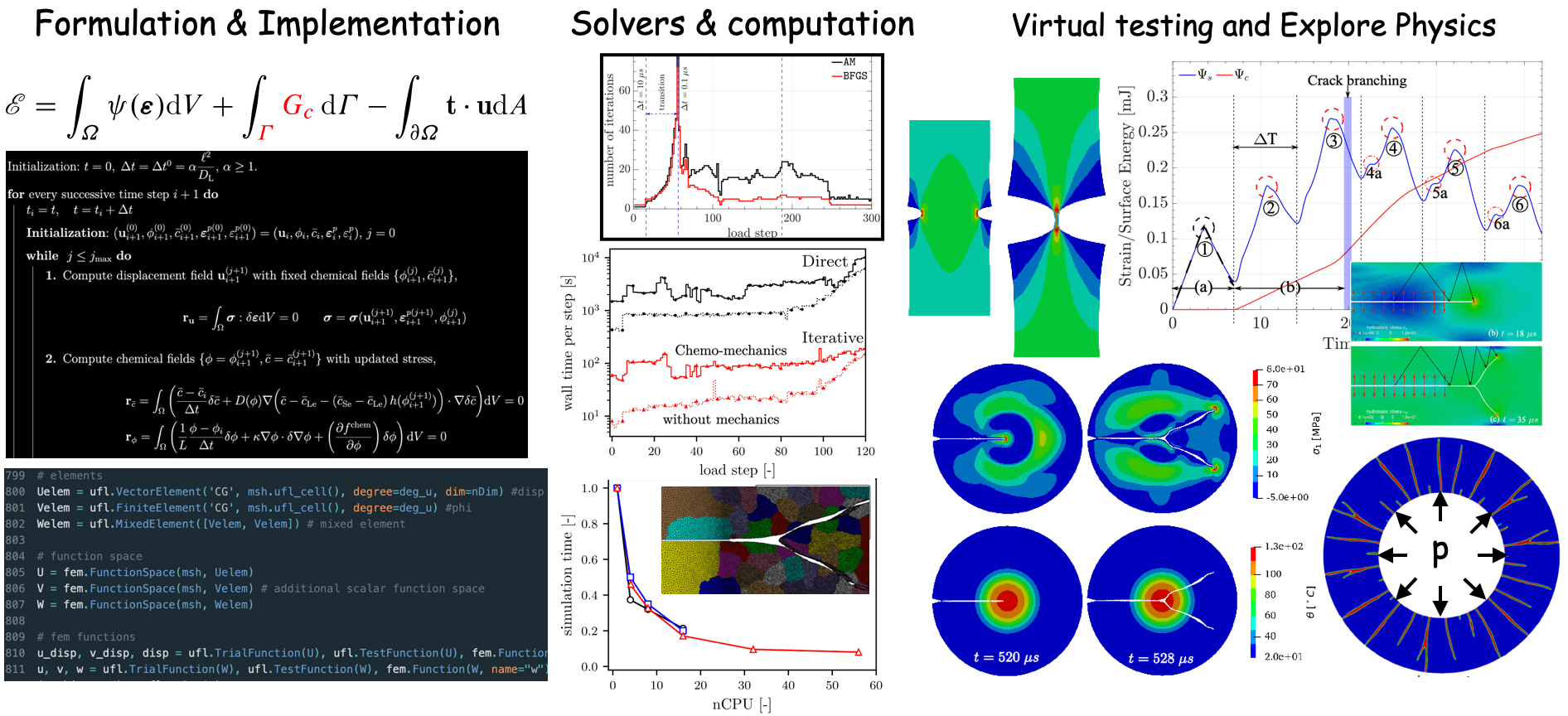
The development of mathematical models in this domain requires a thoughtful selection of kinematic variables and a clear definition of the problem’s configuration, including reference and deformed states. A central aspect of our work involves the computational implementation of these models, which necessitates careful consideration of numerical methods such as the finite element method, finite difference method, or finite volume method. Additionally, the choice of linear solvers — whether direct or iterative – is critical for ensuring efficient and accurate computations.

We place significant emphasis on the use of advanced computational tools and frameworks, including both commercial and open-source software, supported by high-performance computational facilities for large-scale simulations. Particular attention is given to the intricate interplay between the mechanics of fracture processes, computational methodologies, and programming paradigms.

Through detailed studies of the mechanical, computational, and programming aspects of failure phenomena, we aim to address key challenges in fracture mechanics. Our primary focus lies in modelling and simulating crack initiation, propagation, and coalescence under complex loading conditions. This holistic approach bridges theoretical, numerical, and experimental insights, providing an excellent opportunity for young researchers to contribute to advancing our understanding of material failure and fracture behaviour.